
Using the CoordinateMap can be a little hard to get used to. For some users, a mathematical description, free of any python syntax and code design and snippets may be helpful. After following through this description, the code design and usage may be clearer.
We return to the normalization example in Use of the Coordinate Map for spatial normalization and try to write it out mathematically. Conceptually, to do normalization, we need to be able to answer each of these three questions:
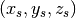 coordinates (
coordinates ( for subject), corresponds to the voxel of data
for subject), corresponds to the voxel of data
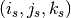 ? This question is answered by subject_im.coordmap.
The actual function that computes this, i.e that takes 3 floats and returns 3
floats, is subject_im.coordmap.mapping.
? This question is answered by subject_im.coordmap.
The actual function that computes this, i.e that takes 3 floats and returns 3
floats, is subject_im.coordmap.mapping.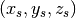 in an anatomical image of the subject, where does it
lie in the Tailarach coordinates
in an anatomical image of the subject, where does it
lie in the Tailarach coordinates 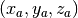 ? This is answered by
the matrix T and knowing that T maps a point in the subject’s world to
Tailarach world. Hence, this question is answered by
subject_world_to_tailarach_world above.
? This is answered by
the matrix T and knowing that T maps a point in the subject’s world to
Tailarach world. Hence, this question is answered by
subject_world_to_tailarach_world above.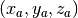 (
( for atlas)
corresponds to the voxel
for atlas)
corresponds to the voxel 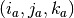 . This question is answered by
tailarach_cmap.
. This question is answered by
tailarach_cmap.Each of these three questions are answered by, in code, what we called a class
called CoordinateMap. Mathematically, let’s define a mapping as a tuple
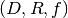 where
where 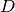 is the domain,
is the domain, 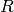 is the range and
is the range and
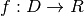 is a function. It may seem redundant to pair
is a function. It may seem redundant to pair
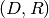 with
with 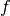 because a function must surely know its domain and
hence, implicitly, its range. However, we will see that when it comes time to
implement the notion of mapping, the tuple we do use to construct
CoordinateMap is almost, but not quite
because a function must surely know its domain and
hence, implicitly, its range. However, we will see that when it comes time to
implement the notion of mapping, the tuple we do use to construct
CoordinateMap is almost, but not quite 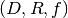 and, in the tuple we
use,
and, in the tuple we
use, 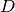 and
and 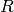 are not reduntant.
are not reduntant.
Since these mappings are going to be used and called with modules like numpy, we should restrict our definition a little bit. We assume the following:
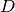 is isomorphic to one of
is isomorphic to one of 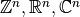 for some
for some 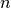 . This isomorphism is determined by a basis
. This isomorphism is determined by a basis
![[u_1,\dots,u_n]](../_images/math/45c0dd45de53a063b38b5c4e3ac9734169710a50.png) of
of 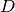 which maps
which maps 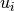 to
to 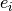 the canonical i-th coordinate vector of whichever of
the canonical i-th coordinate vector of whichever of 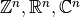 . This isomorphism is denoted by
. This isomorphism is denoted by 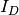 .
Strictly speaking, if
.
Strictly speaking, if 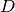 is isomorphic to
is isomorphic to 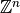 then
the term basis is possibly misleading because
then
the term basis is possibly misleading because 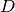 because it is not a
vector space, but it is a group so we might call the basis a set of
generators instead. In any case, the implication is that whatever properties
the appropriate
because it is not a
vector space, but it is a group so we might call the basis a set of
generators instead. In any case, the implication is that whatever properties
the appropriate 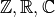 , so
, so 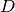 (and
(and
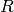 ) has as well.
) has as well.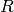 is similarly isomorphic to one of
is similarly isomorphic to one of 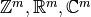 for some
for some 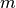 with isomorphism
with isomorphism 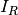 and basis
and basis ![[v_1,\dots,v_m]](../_images/math/114a033bcd01e785a2031a7b781dc174310d390f.png) .
.Above, and throughout, the brackets “[”,”]” represent things interpretable as python lists, i.e. sequences.
These isomorphisms are just fancy ways of saying that the point
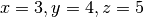 is represented by the 3 real numbers (3,4,5). In this case
the basis is
is represented by the 3 real numbers (3,4,5). In this case
the basis is ![[x,y,z]](../_images/math/7fb8275e9558bb632b9a648d4f52db70997a4b81.png) and for any
and for any 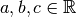
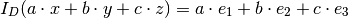
We might call the pairs ![([u_1,...,u_n], I_D), ([v_1,...,v_m], I_R)](../_images/math/c1ba9e4c1ddc2c01d4569e1fa188bfcd24574d30.png) coordinate systems. Actually, the bases in effect determine the maps
coordinate systems. Actually, the bases in effect determine the maps
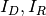 as long as we know which of
as long as we know which of
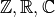 we are talking about so in effect,
we are talking about so in effect,
![([u_1,...,u_n], \mathbb{R})](../_images/math/73791b2386aa464c941fb05f5440cafd0cbc0192.png) could be called a coordinate system. This
is how it is implemented in the code with
could be called a coordinate system. This
is how it is implemented in the code with ![[u_1, \dots, u_n]](../_images/math/9297b2642e12a2430839263d842a179966be6dda.png) being
replaced by a list of strings naming the basis vectors and
being
replaced by a list of strings naming the basis vectors and 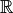 replaced by a builtin numpy.dtype().
replaced by a builtin numpy.dtype().
In our normalization example, we therefore have 3 mappings:
Voxel-to-world (subject) In standard notation for functions, we can write
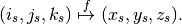
The domain is ![D=[i_s,j_s,k_s]](../_images/math/49aedae2bb92d6b76b540c971a5da1983800139a.png) , the range is
, the range is ![R=[x_s,y_s,z_s]](../_images/math/41c90103486efdd5b6d78bc2f0fc788ad0781c06.png) and the function is
and the function is 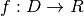 .
.
World-to-world (subject to Tailarach) Again, we can write
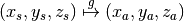
The domain is ![D=[x_s,y_s,z_s]](../_images/math/15ba59a172abdf8a05e0e216a74adeff0a6ec35b.png) , the range is
, the range is ![R=[x_a,y_a,z_a]](../_images/math/dac36656c5402b95eb885889d3576910930e85d9.png) and the function is
and the function is 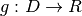 .
.
Voxel-to-world (Tailarach) Again, we can write
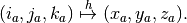
The domain is ![D=[i_a,j_a,k_a]](../_images/math/a5d12c834d1b01f14aef070c90c1bbf88efaa9b6.png) , the range is
, the range is ![R=[x_a,y_a,z_a]](../_images/math/dac36656c5402b95eb885889d3576910930e85d9.png) and the function is
and the function is 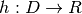 .
.
Note that each of the functions 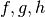 can be, when we know the necessary
isomorphisms, thought of as functions from
can be, when we know the necessary
isomorphisms, thought of as functions from 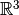 to itself. In
fact, that is what we are doing when we write
to itself. In
fact, that is what we are doing when we write
as a function that takes 3 numbers and gives 3 numbers.
Formally, these functions that take 3 numbers and return 3 numbers can be
written as 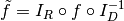 . When this is
implemented in code, it is actually the functions
. When this is
implemented in code, it is actually the functions 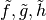 we specify, rather then
we specify, rather then 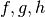 . The functions
. The functions
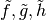 have domains and ranges that are just
have domains and ranges that are just
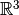 . We therefore call a coordinate map a tuple
. We therefore call a coordinate map a tuple
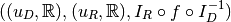
where 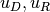 are bases for
are bases for 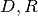 , respectively. It is this
object that is implemented in code. There is a simple relationship between
mappings and coordinate maps
, respectively. It is this
object that is implemented in code. There is a simple relationship between
mappings and coordinate maps
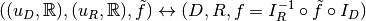
Because 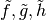 are just functions from
are just functions from
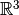 to itself, they can all be composed with one another. But,
from our description of the functions above, we know that only certain
compositions make sense and others do not, such as
to itself, they can all be composed with one another. But,
from our description of the functions above, we know that only certain
compositions make sense and others do not, such as 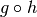 .
Compositions that do make sense include
.
Compositions that do make sense include
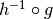 which
which 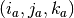 voxel corresponds to the
point
voxel corresponds to the
point 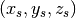 ?
?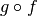 which
which 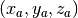 corresponds to the voxel
corresponds to the voxel
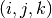 ?
?The composition that is used in the normalization example is 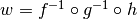 which is a function
which is a function
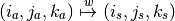
This function, or more correctly its representation 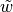 that takes
3 floats to 3 floats, is passed directly to
scipy.ndimage.map_coordinates().
that takes
3 floats to 3 floats, is passed directly to
scipy.ndimage.map_coordinates().
In order to solve our normalization problem, we will definitely need to compose functions. We may want to carry out other formal operations as well. Before describing operations on mappings, we describe the operations you might want to consider on coordinate systems.
Reorder: This is just a reordering of the basis, i.e.
![([u_1,u_2,u_3], \mathbb{R}) \mapsto ([u_2,u_3,u_1], \mathbb{R})](../_images/math/f05069a772042bc1af23bb966e9ec6906ac15270.png)
Product: Topological product of the coordinate systems (with a small
twist). Given two coordinate systems ![([u_1,u_2,u_3], \mathbb{R}),
([v_1, v_2], \mathbb{Z})](../_images/math/d0e08616fe80bac156f4cb94c352e5ffabe32ec0.png) the product is represented as
the product is represented as
![([u_1,u_2,u_3], \mathbb{R}) \times ([v_1, v_2], \mathbb{Z}) \mapsto ([u_1,u_2,u_3,v_1,v_2], \mathbb{R})`.](../_images/math/91765bdb831833fc7995243bb496eae6768c591d.png)
Note that the resulting coordinate system is real valued whereas one of the
input coordinate systems was integer valued. We can always embed
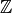 into
into 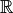 . If one of them is complex
valued, the resulting coordinate system is complex valued. In the code, this
is handled by attempting to find a safe builtin numpy.dtype for the two (or
more) given coordinate systems.
. If one of them is complex
valued, the resulting coordinate system is complex valued. In the code, this
is handled by attempting to find a safe builtin numpy.dtype for the two (or
more) given coordinate systems.
Inverse: Given a mapping 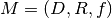 if the function
if the function 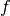 is
invertible, this is just the obvious
is
invertible, this is just the obvious 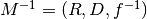 .
.
Composition: Given two mappings, 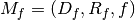 and
and
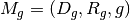 if
if 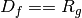 then the composition is well
defined and the composition of the mappings
then the composition is well
defined and the composition of the mappings ![[M_f,M_g]](../_images/math/e5ee75b73b740a65d67ba83e7c4bdbef9f790153.png) is just
is just
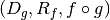 .
.
Reorder domain / range: Given a mapping ![M=(D=[i,j,k], R=[x,y,z], f)](../_images/math/da86e95cdde35a5eb7b3f6969c355af910e2b444.png) you might want to specify that we’ve changed the domain by changing the
ordering of its basis to
you might want to specify that we’ve changed the domain by changing the
ordering of its basis to ![[k,i,j]](../_images/math/55f92a2fdf2cfd4e0da91a5d741d55f31dce9132.png) . Call the new domain
. Call the new domain 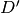 .
This is represented by the composition of the mappings
.
This is represented by the composition of the mappings ![[M, O]](../_images/math/ec59048996ac15f941be2702f609f8556c24570b.png) where
where
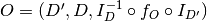 and for
and for 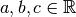 :
:
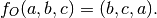
Linearize: Possibly less used, since we know that 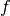 must map one of
must map one of
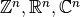 to one of
to one of
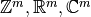 , we might be able
differentiate it at a point
, we might be able
differentiate it at a point 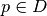 , yielding its 1st order Taylor
approximation
, yielding its 1st order Taylor
approximation
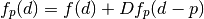
which is an affine function, thus
creating an affine mapping 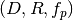 . Affine functions
are discussed in more detail below.
. Affine functions
are discussed in more detail below.
Product: Given two mappings 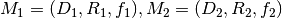 we define their product as the mapping
we define their product as the mapping 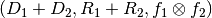 where
where
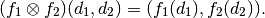
Above, we have taken the liberty of expressing the product of the coordinate
systems, say, ![D_1=([u_1, \dots, u_n], \mathbb{R}), D_2=([v_1, \dots,
v_m], \mathbb{C})](../_images/math/9128573200e2d778b383cfb379e755b66b52f54b.png) as a python addition of lists.
as a python addition of lists.
The name product for this operation is not necessarily canonical. If the two coordinate systems are vector spaces and the function is linear, then we might call this map the direct sum because its domain are direct sums of vector spaces. The term product here refers to the fact that the domain and range are true topological products.
An affine mapping is one in which the function 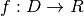 is an
affine function. That is, it can be written as f(d) = Ad + b for
is an
affine function. That is, it can be written as f(d) = Ad + b for 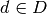 for some
for some 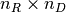 matrix
matrix 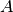 with entries that are in one
of
with entries that are in one
of 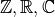 .
.
Strictly speaking, this is a little abuse of notation because 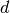 is a
point in
is a
point in 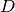 not a tuple of real (or integer or complex) numbers. The
matrix
not a tuple of real (or integer or complex) numbers. The
matrix 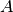 represents a linear transformation from
represents a linear transformation from 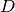 to
to 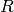 in a particular choice of bases for
in a particular choice of bases for 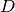 and
and 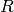 .
.
Let us revisit some of the operations on a mapping as applied to affine
mappings which we write as a tuple 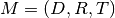 with
with 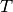 the
representation of the
the
representation of the 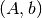 in homogeneous coordinates.
in homogeneous coordinates.
Inverse: If 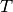 is invertible, this is just the tuple
is invertible, this is just the tuple
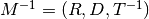 .
.
Composition: The composition of two affine mappings ![[(D_2, R_2,
T_2), (D_1,R_1,T_1)]](../_images/math/b1f4306c7dba4ff6048b9f56ecd82915c8e8868f.png) is defined whenever
is defined whenever 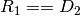 and is the tuple
and is the tuple
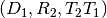 .
.
Reorder domain: A reordering of the domain of an affine mapping
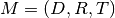 can be represented by a
can be represented by a 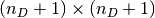 permutation matrix
permutation matrix 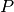 (in which the last coordinate is unchanged –
remember we are in homogeneous coordinates). Hence a reordering of
(in which the last coordinate is unchanged –
remember we are in homogeneous coordinates). Hence a reordering of 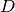 to
to 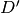 can be represented as
can be represented as 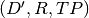 . Alternatively, it is
the composition of the affine mappings
. Alternatively, it is
the composition of the affine mappings ![[M,(\tilde{D}, D, P)]](../_images/math/64735b16dafab94d0e6938319ad8f250d58036a1.png) .
.
Reorder range: A reordering of the range can be represented by a
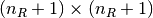 permutation matrix
permutation matrix 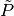 . Hence a
reordering of
. Hence a
reordering of 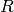 to
to 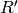 can be represented as
can be represented as 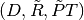 . Alternatively, it is the composition of the affine
mappings
. Alternatively, it is the composition of the affine
mappings ![[(R, \tilde{R}, \tilde{P}), M]](../_images/math/587cfdba22f670d11d5c896a5f8c39bd41d55239.png) .
.
Linearize: Because the mapping 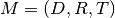 is already affine, this
leaves it unchanged.
is already affine, this
leaves it unchanged.
Product: Given two affine mappings 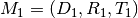 and
and
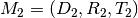 the product is the tuple
the product is the tuple
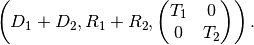
For an Image, by far the most common mappings associated to it are affine, and
these are usually maps from a real 3-dimensional domain to a real 3-dimensional
range. These can be represented by the ubiquitous 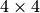 matrix (the
representation of the affine mapping in homogeneous coordinates), along with
choices for the axes, i.e.
matrix (the
representation of the affine mapping in homogeneous coordinates), along with
choices for the axes, i.e. ![[i,j,k]](../_images/math/465e41539be64988731897f2b9ad9ada8b68d607.png) and the spatial coordinates, i.e.
and the spatial coordinates, i.e.
![[x,y,z]](../_images/math/7fb8275e9558bb632b9a648d4f52db70997a4b81.png) .
.
We will revisit some of the operations on mappings as applied specifically to
3-dimensional affine mappings which we write as a tuple 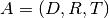 where
where 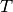 is an invertible
is an invertible 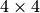 transformation matrix with
real entries.
transformation matrix with
real entries.
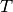 is invertible this is just tuple
is invertible this is just tuple ![(([x,y,z], \mathbb{R}), ([i,j,k], \mathbb{R}), T^{-1})](../_images/math/0da3830175d5bdb7a894b433892beb11b6ae2192.png) .
.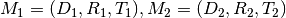 the composition of
the composition of ![[M_2,M_1]](../_images/math/451c7fdf8b639d2bae4678747f1ea3279776b92b.png) yields another
3-dimensional affine mapping whenever
yields another
3-dimensional affine mapping whenever 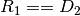 . That is, it yields
. That is, it yields
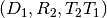 .
.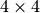 permutation matrix
permutation matrix 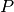 (with its last coordinate not
changing). Hence the reordering of
(with its last coordinate not
changing). Hence the reordering of ![D=([i,j,k], \mathbb{R})](../_images/math/9d43978bce7abec99d62dda373c566baffe805ae.png) to
to
![([k,i,j], \mathbb{R})](../_images/math/ff24a3a4435ad977146faf8e40d40c95cc9cef9e.png) can be represented as
can be represented as ![(([k,i,j],
\mathbb{R}), R, TP)](../_images/math/eb7078180a50b99770670e9bfa1481e9f54a47da.png) .
.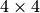 permutation matrix
permutation matrix 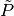 (with its last
coordinate not changing). Hence the reordering of
(with its last
coordinate not changing). Hence the reordering of ![R=([x,y,z],
\mathbb{R})](../_images/math/bd7c2511258b492eefdaa0472f0a10fa5db66a6f.png) to
to ![([z,x,y], \mathbb{R})](../_images/math/c9bdd336fad4a3342c68f58a1dd8881a09137c01.png) can be represented as
can be represented as
![(D, ([z,x,y], \mathbb{R}), \tilde{P}, T)](../_images/math/dcb9a612c25026e050a3ee4d915d9e2ea9d18dbf.png) .
.As noted above coordinate maps are equivalent to mappings through the bijection
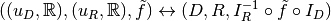
So, any manipulations on mappings, affine mappings or 3-dimensional affine mappings can be carried out on coordinate maps, affine coordinate maps or 3-dimensional affine coordinate maps.
Going from this mathematical description to code is fairly straightforward.
A coordinate system is implemented by the class CoordinateSystem in the module nipy.core.reference.coordinate_system. Its constructor takes a list of names, naming the basis vectors of the coordinate system and an optional built-in numpy scalar dtype such as np.float32. It has no interesting methods of any kind. But there is a module level function product which implements the notion of the product of coordinate systems.
A coordinate map is implemented by the class CoordinateMap in the module
nipy.core.reference.coordinate_map. Its constructor takes two
coordinate has a signature (mapping, input_coords(=domain),
output_coords(=range)) along with an optional argument inverse_mapping
specifying the inverse of mapping. This is a slightly different order from
the 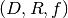 order of this document. As noted above, the tuple
order of this document. As noted above, the tuple
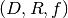 has some redundancy because the function
has some redundancy because the function 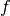 must
know its domain, and, implicitly its range. In numpy, it is
impractical to really pass
must
know its domain, and, implicitly its range. In numpy, it is
impractical to really pass 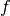 to the constructor because
to the constructor because 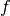 would expect something of dtype
would expect something of dtype 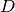 and should return someting of
dtype
and should return someting of
dtype 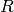 . Therefore, mapping is actually a callable that
represents the function
. Therefore, mapping is actually a callable that
represents the function 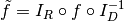 . Of
course, the function
. Of
course, the function 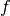 can be recovered as
can be recovered as 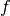 = I_R^{-1} circ
tilde{f} I_D`. In code,
= I_R^{-1} circ
tilde{f} I_D`. In code, 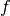 is roughly equivalent to:
is roughly equivalent to:
>>> from nipy.core.api import CoordinateMap, CoordinateSystem
>>> in_cs = CoordinateSystem('ijk', 'voxels')
>>> out_cs = CoordinateSystem('xyz', 'mm')
>>> map = lambda x : x + 1
>>> coordmap = CoordinateMap(in_cs, out_cs, map)
>>> domain = coordmap.function_domain
>>> range = coordmap.function_range
>>> f_tilde = coordmap.function
>>> in_dtype = domain.coord_dtype
>>> out_dtype = range.dtype
>>> def f(d):
... return f_tilde(d.view(in_dtype)).view(out_dtype)
The class CoordinateMap has an inverse property and there are module level functions called product, compose, linearize and it has methods reordered_input, reordered_output.
For more detail on the ideas behind the coordmap design, see coordmp-discussion