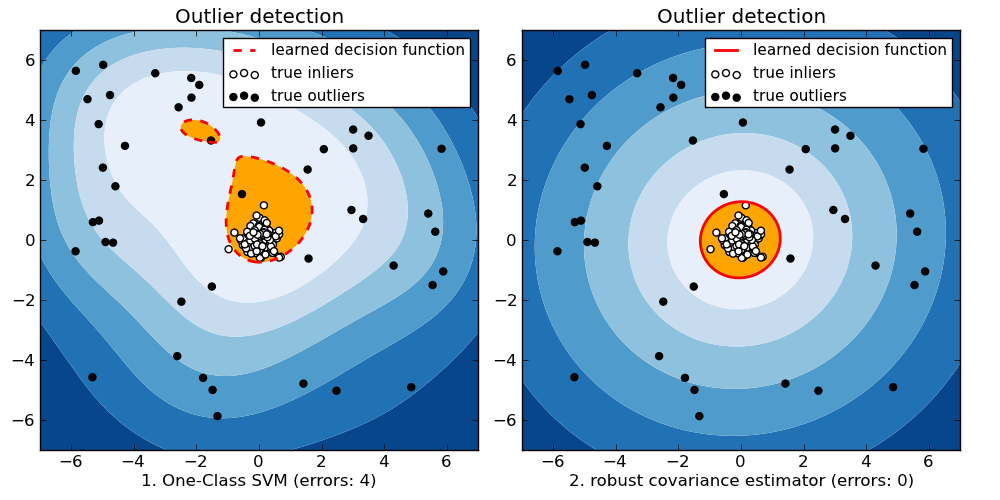
Outlier detection with several methods.¶
This example illustrates two ways of performing Novelty and Outlier Detection when the amount of contamination is known:
- based on a robust estimator of covariance, which is assuming that the data are Gaussian distributed and performs better than the One-Class SVM in that case.
- using the One-Class SVM and its ability to capture the shape of the data set, hence performing better when the data is strongly non-Gaussian, i.e. with two well-separated clusters;
The ground truth about inliers and outliers is given by the points colors while the orange-filled area indicates which points are reported as outliers by each method.
Here, we assume that we know the fraction of outliers in the datasets. Thus rather than using the ‘predict’ method of the objects, we set the threshold on the decision_function to separate out the corresponding fraction.
Python source code: plot_outlier_detection.py
print __doc__
import numpy as np
import pylab as pl
import matplotlib.font_manager
from scipy import stats
from sklearn import svm
from sklearn.covariance import EllipticEnvelop
# Example settings
n_samples = 200
outliers_fraction = 0.25
clusters_separation = [0, 1, 2]
# define two outlier detection tools to be compared
classifiers = {
"One-Class SVM": svm.OneClassSVM(nu=0.95 * outliers_fraction + 0.05,
kernel="rbf", gamma=0.1),
"robust covariance estimator": EllipticEnvelop(contamination=.1),
}
# Compare given classifiers under given settings
xx, yy = np.meshgrid(np.linspace(-7, 7, 500), np.linspace(-7, 7, 500))
n_inliers = int((1. - outliers_fraction) * n_samples)
n_outliers = int(outliers_fraction * n_samples)
ground_truth = np.ones(n_samples, dtype=int)
ground_truth[-n_outliers:] = 0
# Fit the problem with varying cluster separation
for i, offset in enumerate(clusters_separation):
np.random.seed(42)
# Data generation
X1 = 0.3 * np.random.randn(0.5 * n_inliers, 2) - offset
X2 = 0.3 * np.random.randn(0.5 * n_inliers, 2) + offset
X = np.r_[X1, X2]
# Add outliers
X = np.r_[X, np.random.uniform(low=-6, high=6, size=(n_outliers, 2))]
# Fit the model with the One-Class SVM
pl.figure(figsize=(10, 5))
pl.set_cmap(pl.cm.Blues_r)
for i, (clf_name, clf) in enumerate(classifiers.iteritems()):
# fit the data and tag outliers
clf.fit(X)
y_pred = clf.decision_function(X).ravel()
threshold = stats.scoreatpercentile(y_pred,
100 * outliers_fraction)
y_pred = y_pred > threshold
n_errors = (y_pred != ground_truth).sum()
# plot the levels lines and the points
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
subplot = pl.subplot(1, 2, i + 1)
subplot.set_title("Outlier detection")
subplot.contourf(xx, yy, Z,
levels=np.linspace(Z.min(), threshold, 7))
a = subplot.contour(xx, yy, Z, levels=[threshold],
linewidths=2, colors='red')
subplot.contourf(xx, yy, Z, levels=[threshold, Z.max()],
colors='orange')
b = subplot.scatter(X[:-n_outliers, 0], X[:-n_outliers, 1], c='white')
c = subplot.scatter(X[-n_outliers:, 0], X[-n_outliers:, 1], c='black')
subplot.axis('tight')
subplot.legend(
[a.collections[0], b, c],
['learned decision function', 'true inliers', 'true outliers'],
prop=matplotlib.font_manager.FontProperties(size=11))
subplot.set_xlabel("%d. %s (errors: %d)" % (i + 1, clf_name, n_errors))
subplot.set_xlim((-7, 7))
subplot.set_ylim((-7, 7))
pl.subplots_adjust(0.04, 0.1, 0.96, 0.94, 0.1, 0.26)
pl.show()